IT AI Blog
article
Technology

LoRA Without Regret: How to Make Low-Rank Adaptation Match Full Fine-Tuning

6 min read
author
John Smith

TL;DR

LoRA (Low-Rank Adaptation) can match the sample efficiency and final performance of full fine-tuning — but only if you use it correctly. The paper LoRA Without Regret (Schulman et al., 2025) shows:

Why This Matters

Large language models are enormous. Modern base models like Llama-3 or Qwen-3 have tens or hundreds of billions of parameters, sometimes scaling into the trillion range. Full fine-tuning (FullFT) requires updating all weights and optimizer states, which is both memory-hungry and slow.

LoRA offers a different tradeoff: freeze the massive base model, and train only a low-rank correction. This reduces the number of trainable parameters by orders of magnitude and makes serving multiple fine-tuned variants feasible.

But the key question remained: can LoRA actually match FullFT in performance, or is it always a compromise?

Thinking Machines’ work provides the clearest empirical answer so far.

Background: LoRA in One Equation

Image

Instead of updating (W), LoRA learns only (A) and (B), which contain far fewer parameters.

Introduced by Hu et al. (2021), LoRA quickly became the dominant parameter-efficient fine-tuning (PEFT) method, spawning variants such as QLoRA (Dettmers et al., 2023) for 4-bit quantization.

Key Findings from LoRA Without Regret

1. Rank Matters: Capacity and Divergence

Thinking Machines ran supervised fine-tuning experiments on datasets like Tulu-3 and subsets of OpenThoughts-3.

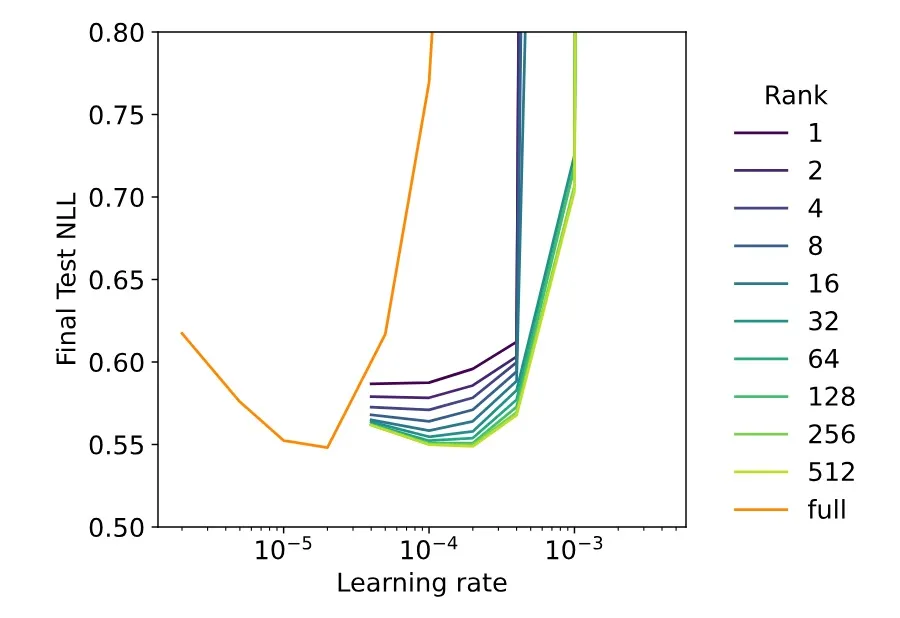
Image
Figure 1. Training loss vs steps for FullFT (black solid) vs LoRA ranks (colored dashed). High-rank adapters remain close; low ranks deviate after a capacity threshold.

2. The 10× Learning Rate Rule

Perhaps the most striking empirical law:

Why?

Image
Figure 2. Validation loss vs learning rate (U-shaped curve). LoRA’s curve minimum lies about one order of magnitude to the right of FullFT’s.

3. Batch Size Sensitivity

LoRA and FullFT behave differently as batch size grows:

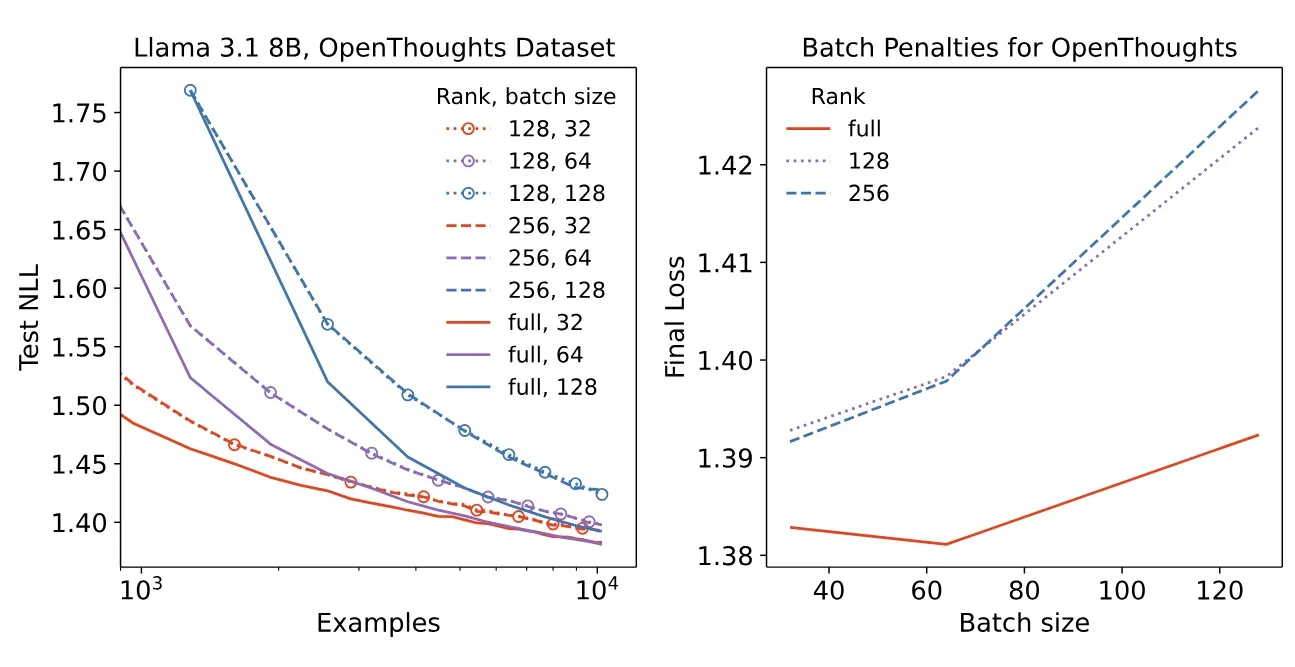Image Figure 3. Final validation loss vs batch size. LoRA (dashed) increasingly lags behind FullFT (solid) as batch size grows.

4. Where to Apply LoRA: Layers Matter

LoRA can be applied to attention projections (Q, K, V, O) and/or MLP blocks.

Findings:

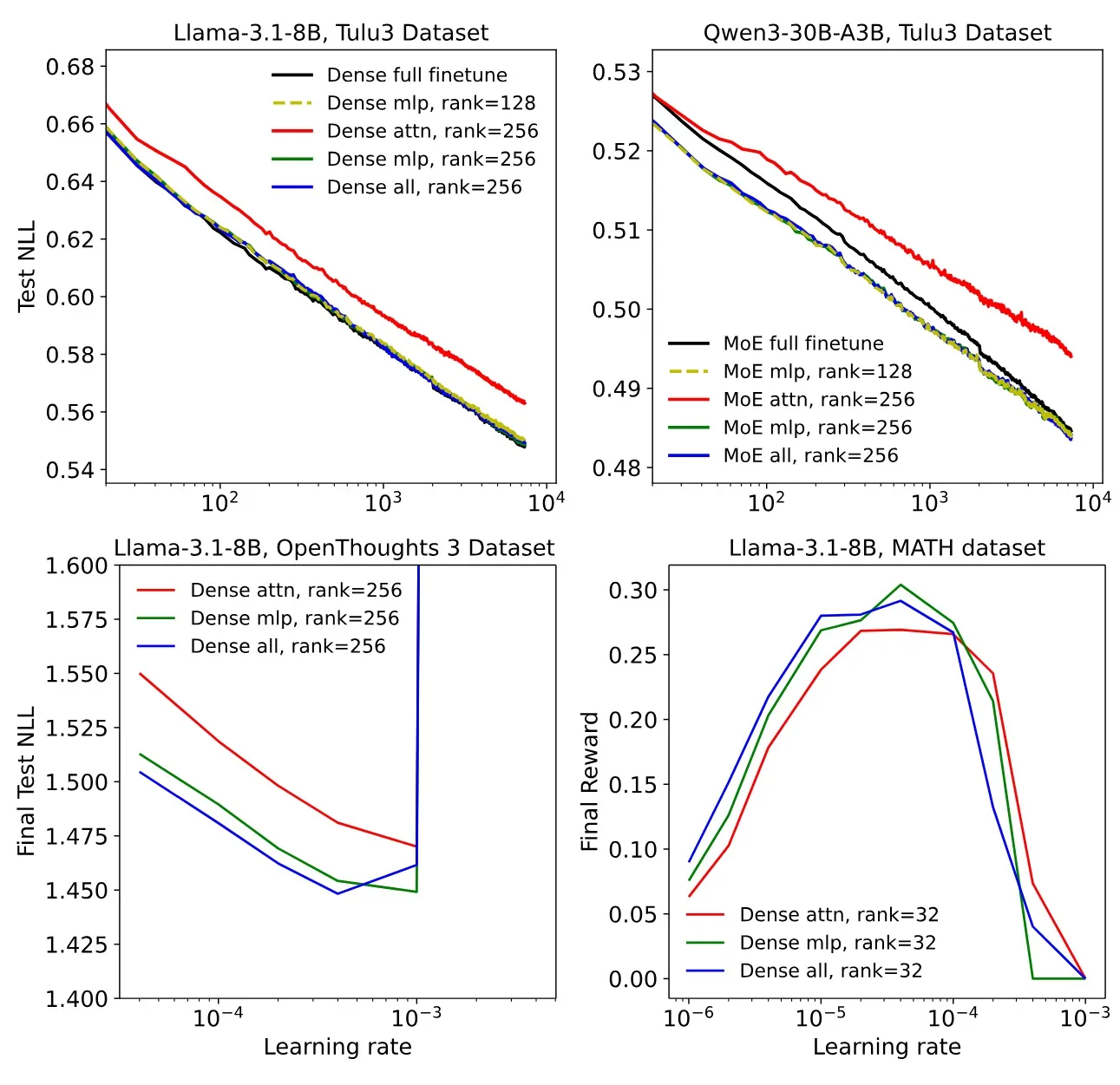Image Figure 4. Performance comparison of LoRA placement: MLP-only > attention-only; all-layers LoRA ≈ FullFT.

5. Reinforcement Learning: LoRA Shines

In reinforcement learning with policy-gradient updates (datasets: MATH, GSM, DeepMath):

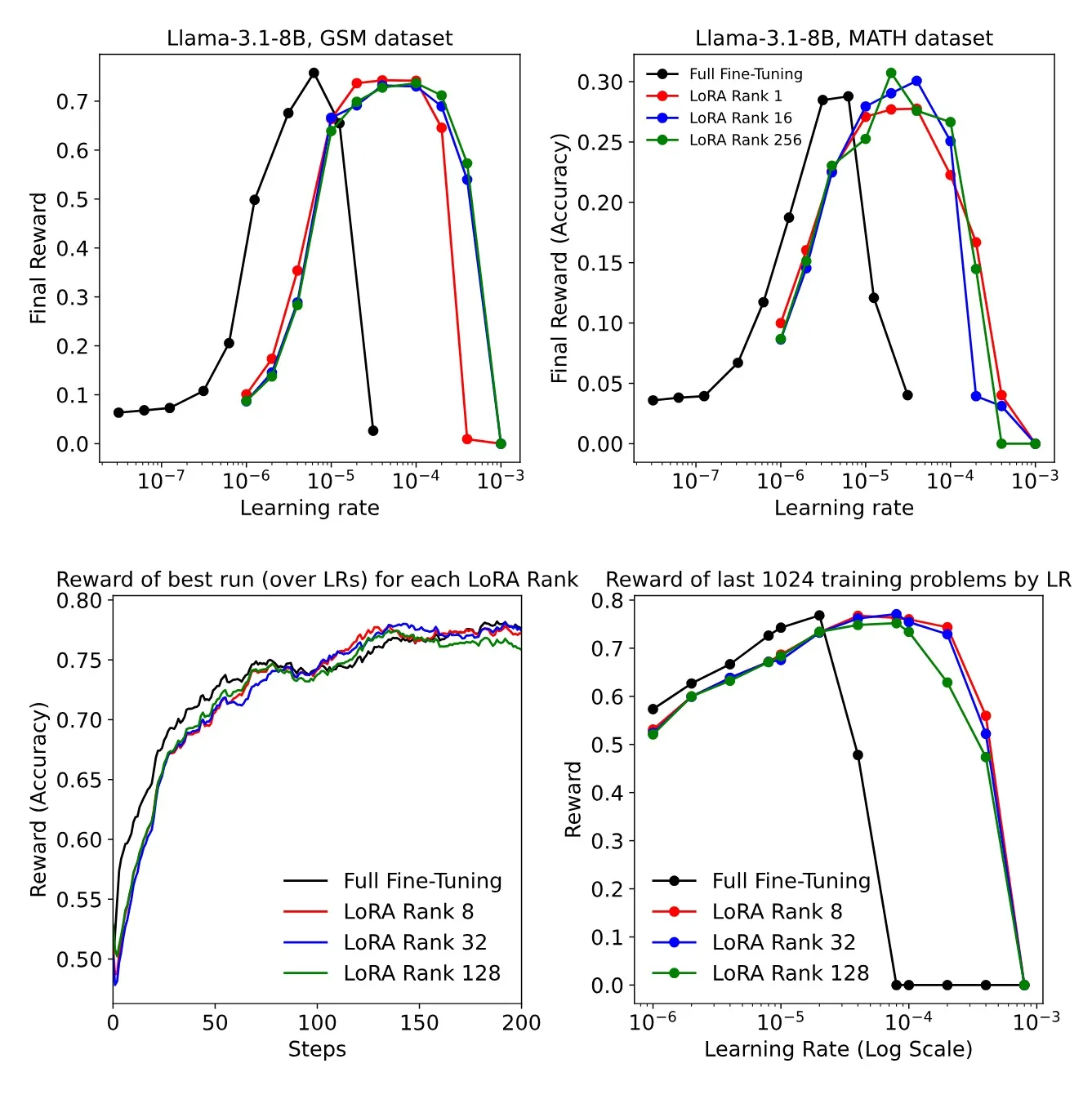Image Figure 5. Reward vs steps for FullFT (solid black) vs LoRA ranks (colored). All LoRA ranks reach similar peak reward.

6. A Predictive Formula for Optimal LR

The authors fitted a function relating optimal LR to:

This gives practitioners a way to estimate optimal LoRA LR without full sweeps.

Takeaway: In practice, though, the “×10 heuristic” is robust enough as a starting point.

Practical Recipe for Engineers

Here’s a consolidated engineering checklist drawn from the paper:

HyperparameterRecommendationNotes
Learning rateStart with FullFT_LR × 10For short runs (≤100 steps), consider ×15
Rank (r)Sweep 256Choose based on dataset complexity; higher = safer
Scaling α32As in paper; effective scale = α / r
Target modulesMLP/MoE (gate, up, down) + attention (q, v)Attention-only insufficient
Batch sizePrefer small/moderate (<512)Large batch hurts LoRA more
RL fine-tuningEven rank=1 is viableWider effective LR range

A Minimal Reproducible Experiment

Below is a minimal Hugging Face + PEFT setup, reflecting the paper’s settings. Swap in your dataset and adjust hyperparameters.

# pip install transformers accelerate peft datasets

from transformers import AutoModelForCausalLM, AutoTokenizer, TrainingArguments, Trainer
from peft import LoraConfig, get_peft_model
import torch

model_name = "meta-llama/Llama-3.1-8b"  # example base model
tokenizer = AutoTokenizer.from_pretrained(model_name, use_fast=False)
model = AutoModelForCausalLM.from_pretrained(model_name, torch_dtype=torch.bfloat16, device_map="auto")

# LoRA config
lora_cfg = LoraConfig(
    r=64,                 # try sweep: [4,16,64,256]
    lora_alpha=32,        # scaling factor
    target_modules=["q_proj","v_proj","gate_proj","up_proj","down_proj"],
    lora_dropout=0.0,
    bias="none"
)
model = get_peft_model(model, lora_cfg)

# Training setup
fullft_lr = 1e-5
lora_lr = fullft_lr * 10

args = TrainingArguments(
    per_device_train_batch_size=32,
    gradient_accumulation_steps=1,
    learning_rate=lora_lr,
    warmup_steps=0,
    num_train_epochs=3,
    logging_steps=10,
    save_strategy="epoch",
    bf16=True,
    optim="adamw_torch"
)

# dataset = load_dataset("tulu3", split="train[:1%]")  # placeholder
# trainer = Trainer(model=model, args=args, train_dataset=dataset, tokenizer=tokenizer)
# trainer.train()

Limitations and Open Questions

Takeaways

References